GIS Concepts
This section discusses various GIS concepts to help the user's comprehension and understanding of those topics.
DE-9IM
DE-9IM or Dimensionally Extended 9-Intersection Model is a topological model and a standard used to describe the spatial relations of two regions. This model uses a matrix of 9 relations cross referencing the two geometries and their common properties: interior, boundary, and exterior. DE-9IM can use one of two domain types when testing spatial relations: Boolean (Egenhofer-Matrix) or Clementini-Matrix.
Boolean domain or Egenhofer-Matrix
When using the boolean domain, each of the 9 relations is either True or False and provides 512 possible combinations (29). Below, a 3-by-3 grid cross references two geometries showing all 9 relations. Note that all relations are true as the two geometries overlap.
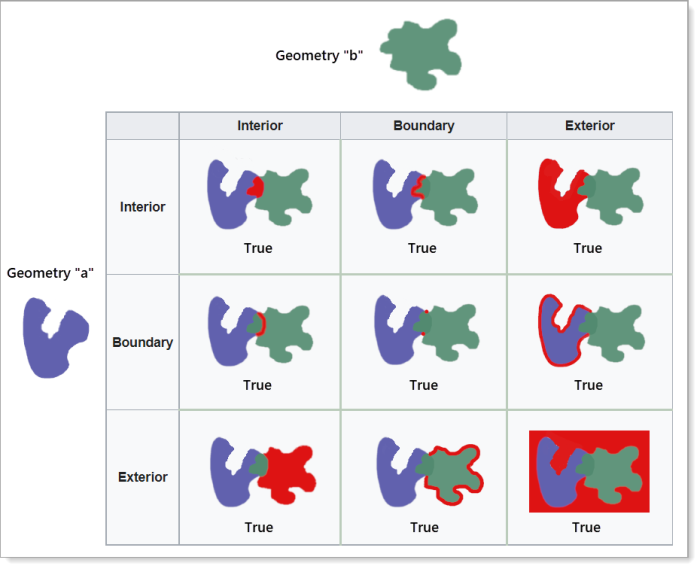
Example of two geometries that have overlapping interiors, boundaries, and exteriors
In the next example, the two geometries only touch at their boundaries and do not overlap.
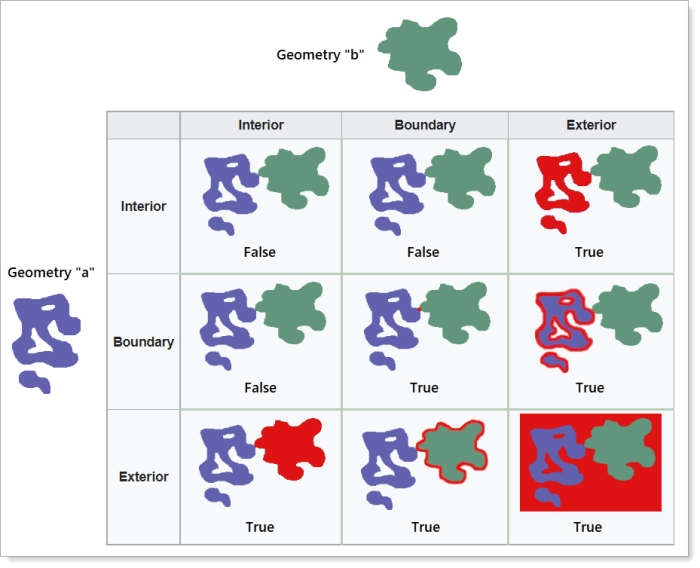
Example of two geometries touching but not overlapping
The Egenhofer-Matrix provides a method for classifying geometry relations. With a 3-by-3 matrix domain, there are 512 possible 2D topologic relations that can be grouped into binary classification schemes. The English language contains schemes or relations, such as "intersects", "touches", and "equals".
Using the Egenhofer-Matrix, relations can be serialized to a text string using the letter "T" for True, "F" for False, and "*" for a wildcard. This string is built by starting at the top left of the grid and working left to right and top to bottom. In the first specific example of overlapping geometries, the text string would be "TTTTTTTTT". As for testing against any overlapping geometry, the text string would be "T*F**F***". In the next specific example of touching geometries with no overlap, it would be represented by the string "FFTFTTTTT". As for testing against any touching geometry, the text string would be "FT*******" or "F**T*****" or "F***T****".
The table below shows 8 relation schemes, their intersection mask, and their definition.
| Relation Scheme | Intersection Mask Serialized String | Definition |
|---|---|---|
| Contains | T*****FF* | a contains b: geometry b lies in a, and the interiors intersect. In other words, a contains b if no points of b lie in the exterior of a, and at least one point of the interior of b lies in the interior of a. |
| Crosses | T*T****** OR T*****T** | a crosses b: they have some but not all interior points in common, and the dimension of the intersection is less than that of at least one of them. |
| Disjoint | FF*FF**** | a and b are disjoint: they have no point in common. They form a set of disconnected geometries. Disjoint is the opposite of Intersects. |
| Equals | T*F**FFF* | a and b are topologically equal. Two geometries are topologically equal if their interiors intersect and no part of the interior or boundary of one geometry intersects the exterior of the other. |
| Intersects | T******** OR *T******* OR ***T***** OR ****T**** | a intersects b: geometries a and b have at least one point in common. Intersects is the opposite of Disjoint. |
| Overlaps | T*T***T** | a overlaps b: they have some but not all points in common, they have the same dimension, and the intersection of the interiors of the two geometries has the same dimension as the geometries themselves. |
| Touches | FT******* OR F**T***** OR F***T**** | a touches b: they have at least one point in common, but unlike the Intersects scheme, their interiors do not intersect. |
| Within | T*F**F*** | a is within b: a lies in the interior of b. |
Clementini-Matrix
In the Clementini-Matrix or the {0,1,2,F} domain, the True operator in the Egenhofer-Matrix is replaced with a value of 0, 1, or 2. This provides 262,144 possible combinations (49). The full domain of possible values used in a mask string include {0,1,2,F,*} and are explained below:
-
0 = Point
-
1 = Line
-
2 = Area
-
F = False (can also be -1)
-
* = Wildcard
In the following example, the grid values utilize values of 0, 1, or 2 instead of T for true, while false values are still denoted by F.
If a value denotes a point, the value "0" is used.
If a value denotes a line, then the value "1" is used.
An area is defined with a value of "2".
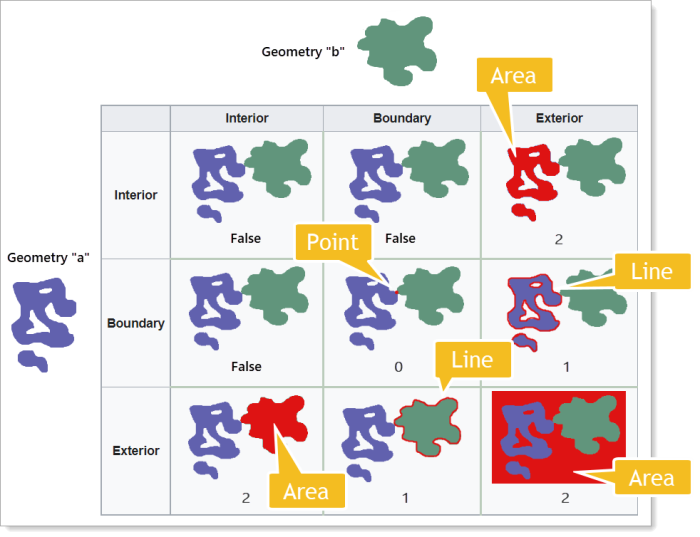
Example of two geometries touching but not overlapping - Clementini-Matrix
In this example of touching geometries with no overlap, the relation between geometries is represented by the string "FF2F01212".
In some examples of geometries that touch but do not overlap, the two boundaries could touch and form a line. In that case, the intersection string would be "FF2F11212". This is because the 5th character in the serialized string represents the boundary of "a" and the boundary of "b".